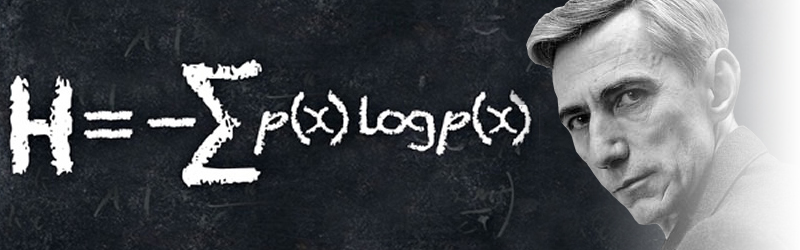
Bandwith and Bitrate

Bandwidth

Why does the sound in a normal old fashioned telephone conversation appear different compared to when you speak to a person face to face? The reason is simply because some of the frequencies contained in the acoustic waves that leaves the mouth of the speaker in one end of the line are lost when transported through the communication system that consists of the microphone, loudspeaker, the electrical components in the telephones and the cables connecting them. The range of frequencies that a communication system can transfer is called its bandwidth. The human ear can detect frequencies between about 20-20000Hz. The air that lies between a sound source and a persons ear supports the propagation of sound waves for all of these frequencies. This gives a bandwidth of of about 20.000Hz for the human auditory system in air. A telephone system is however by construction made so that only frequencies in a range corresponding to the ones present in the human voice are transferred. These roughly lies between 80-250Hz. But the human voice also contains frequencies above and below this frequency span, and if you remove them the voice will sound different, but it will still be good enough for people to understand what is being said.

What about the frequencies that lie outside a systems bandwidth capacity? Are they always completely vanished when the signal reaches the receiver? The answer is no. They are normally just attenuated, or damped, by a certain factor. This factor is often very large however. So for all practical purposes the frequencies outside the bandwidth span can be considered as non existent. But what do we mean by “practical purposes” here. If the frequencies are still there can’t we just detect them with some very sensitive high-tech equipment, amplify them to their normal level and then re-transmit the original sound? This time the answer is yes. Or at least it would be so if it was not for something called Noise.

Noise consists of unwanted random signals that are constantly present in varying degrees in the environment of a communication system. It usually comes from a large number of sources with a wide range of frequencies that adds up to an unpredictable signal background that is added to the true signal. A typical example is thermal noise inside electronics that originates in the heat movement of the electrons that conduct the electric signals. When a signal of a certain frequency becomes as weak as the level of the noise for that frequency (or when the noise becomes as strong as the signal for that matter) the two becomes totally indistinguishable. If you try to amplify the signal you will also amplify the random noise.

Bitrate

So far I have talked about analog  signals and information. Or have I really? Simply stated, digital  information consists of discrete pieces that must be collected and assembled at the receiving end in order to recreate the full message. The only thing that matters is that the system in good enough for the receiver to be able to distinguish one piece of information from an other. But how is it with human speech? If you think about it, it actually consists of discrete pieces. Words! They are discrete entities that we use to communicate with each other. In a voice conversation, what is important to convey a message is that the quality of the system is good enough for us to be able to distinguish one specific word from an other. The fact that there are very many  words doesn’t really change the fact that they are discrete and therefor human language in a sense is a form of digital communication. In written communication words are divided into even smaller pieces. Letters or other kinds of symbols! In the design of modern computers this process of dividing discrete information into smaller and smaller pieces has been taken as far as it is possible to do. Left are only two states or bits, usually just called 1 and 0  ^†.

Now, bitrate simply means how many bits of information a system is able to transfer each second. Why is this so often referred to as bandwidth. How do you convert Bandwidth to Bitrate? How are the two connected?

Well, that depends on the quality of your communication system. In a completely noise-free system with the capability to transmit and receive (and distinguish) two frequencies infinitely closely separated you can theoretically send an arbitrary amount of information in an instance, also in the case of a limited bandwidth.

This could for example be done by dividing the full bandwidth into N narrower bands and let the frequency in the center of each band represent a specific message.

For N = 8, frequency no. 1 could then correspond to the message 000, frequency no. 2 to the message 001, no. 3 to 010 etc. For any possible 3-bit message you can just select the appropriate frequency to transmit.

In your perfect communication system the receiver would be able to distinguish two nearby frequencies even if N is very large and they are very close to each other. However, in order to increase the message size with 1 bit you must double N. This of course puts a heavy constraint on how long the message can be in any real and imperfect system, and you must therefore divide a long message into smaller pieces (called symbols) that are transmitted one after each other. This example nevertheless illustrates that there is no simple one to one relationship (unit conversion) between bandwidth and bit-rate.

Also. For any kind of channel and physical quantity representing a distinct symbol value (e.g. a voltage level representing 0 and 1 in a copper wire), signals with frequency components outside the bandwidth-limit are just suppressed by a factor, not completely zero. So, in an ideal noise-free system you can always reconstruct the signal perfectly if you know the frequency response (which you of course can measure). Take a simple 1010101 … sequence for instance. Its fundamental frequency (same as the bit-rate in this case) will always be detectable as a sine wave no matter the bit-rate. It will just be very attenuated at rates above the bandwidth limit when reaching the receiver, but since you don’t have any noise you will be able to measure it.

In the presence of noise however, there are two obvious things you can do to save the day:

• Transmit with an increased power. Since the interesting aspect of the noise is its amplitude compared to the signal amplitude, you effectively lower the noise if you can increase the signal without increasing the noise. The bandwidth does not prevent you from doing this. For short: No matter the bandwidth, you can further increase the bit-rate by lowering the noise through an increase of the signal power.
• Transmit each bit for a longer time in order for the receiver to be able to measure/sample the signal level (e.g. voltage) for a longer time to get a value accurate enough to distinguish it from other levels. And voila! here is your combined noise and bandwidth dependent bit-rate. Transmitting each bit for a longer time is the definition of a lower rate. By increasing the bandwidth, more frequency components will get amplified with respect to the noise and you will not need as long time (or as many samples) to get an accurate measurement of the level.

The upper bit-rate limit in the case where there is noise is often stated as the Channel Capacity

^†  There is much to be said about how humans represent information. I think you can make a good argument that we actually treat a substantial part of the information we receive in a "digital" manner. Visual information we often get in the form of discrete objects that we associate and represent with various entities that we have given a certain meaning via our collected experiences. We get confused when our vision is compromised to the degree that we can no longer distinguish a category of an object from a different category of objects. Not totally unlike when a computer is not able to distinguish a 1 from a 0. This is an interesting subject. It gets more difficult when we look at how emotions are transferred in say a human telephone conversation. This is only partly based us being able to understand and distinguish the discrete words being said, other qualities of the sound comes into play here.