Exponential Lifetime

Elementary particles, atoms and even molecules do not age like the big macroscopic objects that they are the constituents of, such as biological cells, cars, humans and stars. The physical matter we see around us consists mainly of stable particles, which means that they don’t cease to exist for very long times. They have nevertheless been created and started their existence at some point in the past. Some sooner than others. Interestingly enough there is however no way to even in principle tell for how long an individual atom or elementary particle have existed by just inspecting it. The only way to know is if you actually witnessed when it was created. This in turn is connected to the fact that the particles that do cease to exist by decaying into other particles, have a very characteristic life time expectancy that is a falling exponential to its statistical nature.

Ordinary macroscopic objects are all complicated composite entities, and the probability of them disintegrating and ending their existence as the objects we know them, typically gets higher the longer they have existed or the more they have been effected by their environment. One can by observation and inspection tell if a car have existed longer, or is closer to the end of its existence, than an other car. This works also in the case when they appeared to be perfectly identical at the time of their production or birth, when they were rolled out from the car factory.

This property is closely connected to the fact that one can separate one distinct object from another (even if you at some point have lost track of their whereabouts). No two macroscopic objects are ever exactly perfectly identical. Even two brand new cars can be distinguished after close inspection. The reason for this is that they have a complicated internal structure that shows signs of wear and tear. Even if you need to use a magnifying-glass to see small differences you will always find them.

Two elementary particles of the same type on the other hand, are identical and non-separable in a more fundamental sense. There is for instance no way, that we know of, to even in principle tell if one particle is older than another. In a sense they are as ultimately simple as physical objects can be. If one could tell them apart, a particle would have to have some internal structure that kept track of its history (like the bumps and scratches on a car). One could of course argue that there might be such internal structure which we just haven’t found yet. That the particles really have some complicated internal wear and tear leaving traces that could be used to conclude how old they are. It however seems that not even nature itself can keep track of how old an elementary particle is.

How can we know this (what do I even mean by this)? Well, a natural consequence of this property is that a particle which was created one second ago will have exactly the same chance of ending its existence and decaying into other particles within the next second as a particle that was created one hour, one year or one nanosecond ago. Put an other way, the probability to decay within the next time interval (say the next second) is independent of when that time interval begins with respect to the time of creation of the particle. This in turn gives rise to what we can call exponential lifetime or exponential decay.

In the figure below the exponential decay is illustrated. On the x-axis is time and the area under the curve between time 0 (when one starts to observe the particle) and some arbitrary time, shows the probability that the particle will decay within that time interval. What is amazing here is that it doesn’t matter how old the particle is when you start to observe it.

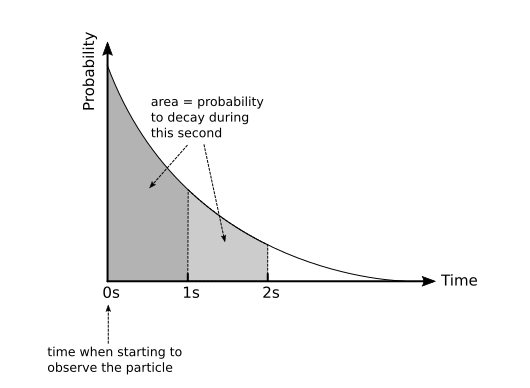
It is clearly seen from the figure that the probability to decay within the first second is higher than decaying within the second one. But wait! How can that be when we have said the the probability should be independent of time. Well, one have to take into account here that the particle must first survive the first second in order to even be able to decay during the second one, and since the probability of surviving the first second is lower than 1, it lowers the overall probability that the particle will both survive until the second interval and also decay inside it.

The important point here is that the time intervals are independent of each other. A particle has no memory what so ever about its past. This means that the probability to survive for the next 2 seconds is the same as the probability to survive for the next second times (x) the probability to survive for an other second after that (which then is exactly the same as surviving the first second). One can of course consider smaller time intervalls: The probability to survive for the next 1/2 second, times the next half second after that, times the next 1/2 second after that etc. Now, the probability to survive for any time period must be a number smaller than or equal to 1 (exactly 1 for stable particles that never decay). Actually the probability to survive for a certain time is exactly 1 minus the probability to decay during the same time (they are two mutually exclusive options). This means that the more time periods you stack on top of each other (multiply by a number smaller than 1), the smaller the chance is that the particle will survive all of them.

It is just like trying to pass a number of independent and very dangerous obstacles, each one having the same probability to end your life, and where the number of obstacles you have previously passed have no effect on your ability to pass the next one. In fact, if you for an everyday macroscopic object choose to only look at certain specific causes of it being destroyed (it could for instance be crashes in the case of cars). Then the probability of an object having its existence end in that particular way might very well follow an exponential distribution.

Now, it might be a bit discouraging to think that, if you are going to die in a random accident, it looks like it is more likely to happen sooner rather than later. But again, one must then keep in mind that the lower probability for later occurrences are lowered by taking into account the probability that you have already died in an earlier accident. The scales are reset every moment that have passed without any accidents happening … luckily!